Изучая кинематику, мы учимся описывать механическое движение – изменение положения тела относительно других тел с течением времени. Для пояснения очень важных слов «относительно других тел» приведём пример, в котором вам потребуется применить воображение.
Допустим, мы сели в автомобиль и выехали на дорогу, ведущую на север. Оглядимся вокруг. Со встречными автомобилями всё просто: они всегда приближаются к нам с севера, проезжают мимо нас и удаляются на юг (взгляните на рисунок – голубой автомобиль слева).

С попутными машинами сложнее. Те автомобили, которые едут быстрее нас, приближаются к нам сзади, обгоняют и удаляются на север (например, серое авто в центре). Но автомобили, которые обгоняем мы, приближаются к нам спереди и удаляются от нас назад (красное авто справа). То есть попутные автомобили относительно нас могут удаляться на юг в то же самое время, когда относительно дороги едут на север!
Итак, с точки зрения водителя и пассажиров нашей машины (внизу на рисунке её синий капот) обгоняемый красный автомобиль удаляется на юг, хотя, с точки зрения мальчика на обочине дороги, этот же автомобиль едет на север. Кроме того, мимо мальчика красное авто «пролетит со свистом», а мимо нашей машины – «медленно уплывёт» назад.
Таким образом, движение тел может выглядеть по-разному с точек зрения различных наблюдателей. Это явление – относительность механического движения. Оно проявляется в том, что быстрота, направление и траектория одного и того же движения различны для разных наблюдателей. Первые два различия (в быстроте и направлении движения) мы только что проиллюстрировали на примере автомобилей. Далее мы покажем различия в виде траектории одного и того же тела для разных наблюдателей (см. рисунок с яхтами).
Напомним: кинематика создаёт математическое описание движения тел. Но как это сделать, если движение выглядит по-разному с точек зрения различных наблюдателей? Чтобы была определённость, в физике всегда выбирают систему отсчёта.
Системой отсчёта называют часы и систему координат, связанные с телом отсчёта (наблюдателем). Поясним это примерами.
Вообразим, что мы едем в поезде и роняем предмет. Он упадёт к нашим ногам, хотя даже при скорости 36 км/ч поезд ежесекундно передвигается на 10 метров. Вообразим теперь, что на мачту яхты взобрался матрос и роняет ядро (см. рисунок). Нас также не должно смутить, что оно упадёт к основанию мачты, несмотря на то что яхта плывёт вперёд. То есть в каждый момент времени ядро движется и вниз, и вперёд вместе с яхтой.
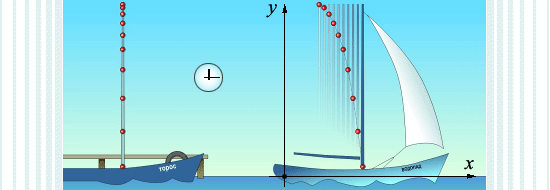
Итак, в системе отсчёта, связанной с яхтой (назовем её «палуба»), ядро движется только по вертикали и проходит путь, равный длине мачты; траектория ядра – отрезок прямой. Но в системе отсчёта, связанной с берегом (назовем её «пристань»), ядро движется и по вертикали, и вперёд; траектория ядра представляет собой ветвь параболы, и путь явно больше, чем длина мачты. Вывод: траектории и пути одного и того же ядра различны в различных системах отсчёта: «палуба» и «пристань».
А что со скоростью ядра? Поскольку это одно и то же тело, то время его падения в обеих системах отсчёта мы считаем одинаковым. Но так как пройденные ядром пути различны, то и скорости одного и того же движения в разных системах отсчёта различны.