Стробоскопическая фотография в предыдущем параграфе показывает, что свободно падающий шарик движется с ускорением. Различных тел, движущихся с ускорением, вокруг нас множество. Это, например, нога футболиста перед ударом по мячу, взлетающая с космодрома ракета, отъезжающий от станции поезд и так далее.
По аналогии с формулой мгновенной скорости в физике вводят формулу, выражающую определение мгновенного ускорения:
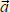 = = | . Δ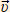 . . | 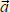 – мгновенное ускорение, м/с² – мгновенное ускорение, м/с²Δ 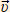 – изменение скорости, м/с ( если Δt→0 ) – изменение скорости, м/с ( если Δt→0 )Δt – стремящийся к нулю интервал времени, с | |||
| Δt |
В школьной физике изучают только такие движения, для которых модуль мгновенного ускорения не меняется с течением времени. Поэтому вместо «мгновенное ускорение» часто говорят короче: «ускорение». Например, ускорение поезда, ускорение ракеты, летящего мяча и так далее.
Вспомним, что при равноускоренном движении мгновенная скорость за любые равные интервалы времени изменяется одинаково (см. § 12-з). Поэтому, если равные изменения мгновенной скорости поделить на равные интервалы времени, мы получим равные ускорения. Другими словами, при равноускоренном движении ускорение постоянно (как по числовому значению, так и пространственному направлению), значит, интервал времени наблюдения может быть любым. И тогда из формулы мгновенного ускорения мы получим определение ускорения:
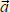 = = | Δ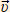 | = | 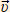 – – 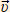 o o | = | 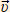 – – 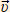 o o | |
| Δt | t – to | t |
, принимая момент времени to = 0 .
Выпишем начало и конец получившегося равенства и выразим скорость:
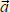 = = | 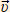 – – 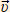 o o | ⇒ | 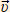 = = 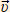 o + o + 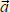 t t | |
| t |
, если ускорение постоянно.
Для движения вдоль осей X и Y эта формула может быть записана с использованием проекций векторов на координатные оси:
υx = υox + ax t и υy = υoy + ay t
Как видно из этих равенств, при равноускоренном движении проекции мгновенной скорости зависят от времени по линейному закону, то есть описываются линейными функциями вида y = kx + b.
Ускорение свободного падения. Взглянем ещё раз на чертёж с «векторным треугольником» и последний абзац § 12-з. Обратим внимание: вектор изменения скорости свободно падающего шарика, а значит, и вектор ускорения свободного падения направлен вниз и не зависит от скорости тела. Подтвердим это вторым способом.

Проделаем опыт. В стеклянную трубку с краном помещены скомканный лист бумаги и камешек. Сначала кран трубки открыт, и внутри неё находится атмосферный воздух. Поэтому при переворачивании трубки бумага падает с меньшим по модулю ускорением. Затем воздух откачивают, создавая в трубке вакуум, а кран закрывают. Теперь бумага падает с тем же ускорением, что и камень. Опыт нам продемонстрировал, что ускорение свободного падения одинаково для всех тел. В физике свободным падением называют движение тела при действии только силы тяжести.
Если на тело действуют сравнительно малые силы, препятствующие свободному падению, то их действием можно пренебречь. Тогда измерения показывают: модуль ускорения свободного падения всех тел вблизи поверхности Земли равен 9,8 м/с². Это значение вам уже знакомо из 7 класса как «коэффициент силы тяжести» (см. § 3-г). Вспомнив определение 1 ньютона (см. § 3-а), вы поймёте, что уже известное вам значение 9,8 Н/кг – это именно 9,8 м/с².
Для вычисления (измерения) любых ускорений тел, и ускорения свободного падения в частности, вполне можно использовать метод стробоскопического фотографирования.