Завершая изучение основ кинематики, рассмотрим движение, которое является равномерным и ускоренным одновременно, поскольку вектор мгновенной скорости меняется особым образом.
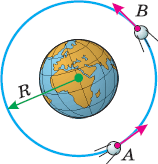
Рассмотрим спутник, равномерно летящий по круговой орбите вокруг Земли: за равные интервалы времени он пролетает равные части пути, поэтому мгновенная скорость спутника сохраняет свой модуль. То есть можно говорить о наличии скорости равномерного движения (см. § 12-д). Однако при этом мгновенная скорость непрерывно меняет направление.
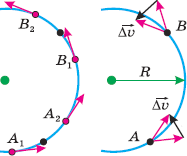
Найдём, куда направлен вектор изменения мгновенной скорости в двух произвольных точках траектории А и В. Для этого сделаем новый чертёж, обозначив Землю зелёной точкой, а спутник – красной. Выберем вблизи положений спутника А и В пары точек А1, А1 и В1, В2. Изобразим в каждой из них вектор мгновенной скорости спутника (см. чертёж). Пользуясь «правилом треугольника» для нахождения разности двух векторов, построим и обозначим векторы изменения мгновенной скорости (см. правую часть чертежа).
Построение при Δt→0 показывает, что при равномерном движении по окружности вектор изменения мгновенной скорости, оставаясь постоянным по модулю, в любой точке траектории направлен к центру окружности. То есть существует так называемое центростремительное ускорение, сонаправленное с вектором изменения мгновенной скорости и имеющее модуль, который всегда можно вычислить по следующей формуле:
| a = | . υ² . | a – модуль центростремительного ускорения, м/с² υ – модуль скорости равномерного движения, м/с R – радиус окружности или её дуги, м | |||
| R |
Эта формула выводится из геометрических построений и рассуждений. Они сложны, поэтому мы приводим формулу без вывода. Важно: в отличие от ранее рассмотренных, в этой формуле присутствует не вектор и даже не проекция мгновенной скорости, а её модуль.
В наше время на балконах и крышах домов нередко можно видеть антенны-«тарелки», принимающие спутниковый телевизионный сигнал. Не кажется ли вам удивительным, что спутники, на которые направлены антенны, неподвижно «висят» в небе?

Вспомним: Земля обращается вокруг своей оси за 24 часа. И если спутник будет облетать вокруг нашей планеты с периодичностью 24 часа, то он будет двигаться синхронно с вращением Земли, всё время «пролетая» над одной и той же точкой земной поверхности. Такие спутники и их орбиты называются геостационарными.
Известно: геостационарные орбиты находятся на высоте около 30000 км над поверхностью Земли. Подсчитаем, с какой скоростью летают по ним спутники. Длину орбиты найдём по формуле длины окружности: l = 2πR. Время оборота по орбите 24 часа, а радиус Земли около 6000 км.
| υ = | l | = | 2πR | = | 2 · 3,14 · ( 30000 + 6000 ) км | ≈ 9420 км/ч | |
| Δt | T | 24 ч |
| В ходе этого рассуждения мы вывели формулу для расчёта модуля скорости тела, равномерно движущегося по окружности: | υ = | 2πR | ||
| T |
| Тогда модуль центростремительного ускорения тела при его равномерном движении по окружности можно вычислить по формуле: | a = | 4π²R | ||
| T² |
| a = | υ² | = | … | = | 4π²R | = | 4 · 3,14² · ( 30000 + 6000 ) км | ≈ 0,2 м/с² | |
| R | T² | ( 24·60·60 с )² |
Вычисленное значение показывает, что на геостационарной орбите вектор мгновенной скорости спутника, оставаясь постоянным по модулю, ежесекундно меняется на 0,2 м/с по направлению.