При равноускоренном движении справедливы следующие уравнения, которые мы приводим без вывода:
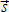 = = 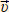 o t + ½ o t + ½ 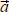 t² t² | ⇒ | sx = υox t + ½ ax t² | ||
| sy = υoy t + ½ ay t² |
Как вы понимаете, векторная формула слева и две скалярные формулы справа равноправны. С точки зрения алгебры, скалярные формулы означают, что при равноускоренном движении проекции перемещения зависят от времени по квадратичному закону. Сравните это с характером проекций мгновенной скорости (см. § 12-з).
Зная, что sx = x – xo и sy = y – yo (см. § 12-е), из двух скалярных формул из правой верхней колонки получим уравнения для координат:
| x = xo + υox t + ½ ax t² | и | y = yo + υoy t + ½ ay t² |
Поскольку ускорение при равноускоренном движении тела постоянно, то координатные оси всегда можно расположить так, чтобы вектор ускорения был направлен параллельно одной оси, например оси Y. Следовательно, уравнение движения вдоль оси X заметно упростится:
x = xo + υox t + ( 0 ) и y = yo + υoy t + ½ ay t²
Обратите внимание, что левое уравнение совпадает с уравнением равномерного прямолинейного движения (см. § 12-ж). Это означает, что равноускоренное движение может «складываться» из равномерного движения вдоль одной оси и равноускоренного движения вдоль другой. Подтверждением этому служит опыт с ядром на яхте (см. § 12-б).
Задача. Вытянув руки, девочка подбросила шар. Он поднялся на 80 cм и вскоре упал к ногам девочки, пролетев 180 cм. С какой скоростью шар был подброшен и какую скорость шар имел при ударе о землю?
Рекомендация. Для решения задач, в которых не дано время и не просят его найти, очень удобно применять не содержащую время формулу для квадрата проекции мгновенной скорости. Выведем эту формулу.
Возведём в квадрат обе части уравнения для проекции на ось Y мгновенной скорости: υy = υoy + ay t (см. § 12-и). Получим равенство:
υy² = ( υoy + ay t )² = υoy² + 2 υoy ay t + ay² t²
Вынесем за скобки множитель 2 ay только для двух правых слагаемых:
υy² = υoy² + 2 ay ( υoy t + ½ ay t² )
Заметим, что в скобках получилась формула для вычисления проекции перемещения: sy = υoy t + ½ ay t². Заменяя её на sy , получим:
| υy² = υoy² + 2 ay sy |
Решение. Сделаем чертёж: ось Y направим вверх, а начало координат поместим на земле у ног девочки. Применим выведенную нами формулу для квадрата проекции скорости сначала в верхней точке подъёма шара:

0 = υoy² + 2·(–g)·(+h) ⇒ υoy = ±√¯2gh = +4 м/с
Затем при начале движения из верхней точки вниз:
υy² = 0 + 2·(–g)·(–H) ⇒ υy = ±√¯2gh = –6 м/с
Ответ: шар был брошен вверх со скоростью 4 м/с, а в момент приземления имел скорость 6 м/с, направленную против оси Y.
Примечание. Надеемся, вы понимаете, что формула для квадрата проекции мгновенной скорости будет верна по аналогии и для оси X:
| υx² = υox² + 2 ax sx |
Если движение одномерное, то есть происходит только вдоль одной оси, можно пользоваться любой из двух формул в рамках.