Современная техника требует большой точности в описании движений, например, при посадке самолёта или стыковке космических кораблей. Поскольку они движутся непрямолинейно и неравномерно, нужно знать их скорости в каждое мгновение в каждой точке траектории.
Как любая траектория состоит из бесконечного числа точек, так и любой интервал времени состоит из бесконечного числа мгновений. И если интервал времени стремится к нулю, превращаясь в «мгновение», то уже известную вам формулу можно применить для определения мгновенной скорости тела:
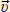 = = | . 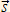 . . | 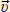 – мгновенная скорость, м/с – мгновенная скорость, м/с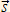 – перемещение тела, м ( если Δt→0 ) – перемещение тела, м ( если Δt→0 )Δt – стремящийся к нулю интервал времени, с | |||
| Δt |
Итак, мгновенная скорость – векторная физическая величина, равная отношению перемещения к интервалу времени, за который это перемещение произошло, если интервал времени стремится к нулю.
Интервал времени – всегда положительный скаляр, поэтому вектор мгновенной скорости всегда сонаправлен с вектором перемещения при Δt→0.
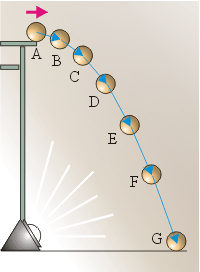
Для изучения быстрых движений применяют прибор стробоскоп, создающий частые вспышки света через равные интервалы времени (см. рисунок). Сфотографируем полёт тяжёлого шарика со стола при различных частотах вспышек. Все фотографии показывают, что траектория – это ветвь параболы, состоящая из отдельных «точек».
Например, от точки A за Δt→0 шарик совершит бесконечно малое перемещение вправо, поэтому и мгновенная скорость в точке A тоже будет направлена вправо.
Делая интервалы между вспышками света стробоскопа всё меньше и меньше, мы построим чертёж, показывающий, что векторы мгновенных скоростей всегда располагаются по касательным к траектории тела (см. чертёж справа, красные векторы).
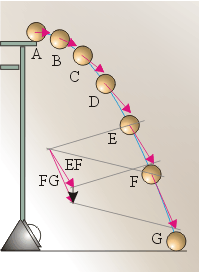
Взгляните: векторы мгновенной скорости меняются не только по направлению, но и по модулю: числовое значение мгновенной скорости возрастает с течением времени. Откуда мы можем это знать? Конечно, только проведя измерения перемещений шарика по его стробоскопическим фотографиям и поделив их на интервалы времени между вспышками света. Эти измерения и вычисления позволят нам начертить векторы скорости в условном, выбранном нами для этого чертежа, масштабе (см. чертёж справа).
Такое движение тела, при котором его мгновенная скорость за любые равные интервалы времени изменяется одинаково, называется равноускоренным движением.
Поскольку мгновенная скорость тела является векторной величиной, то изменение мгновенной скорости – векторная разность: 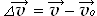 .
.
Найдём векторную разность двух последних векторов чертежа по «правилу треугольника», изученному нами ранее (см. § 12-г). Параллельным переносом скопируем векторы из точки E и точки F на свободное место на чертеже левее, совместив начала векторов. Построим вектор разности, проведя его от вычитаемого вектора к уменьшаемому вектору. Получим вектор изменения скорости шарика между точкой E и точкой F (мы его показали чёрным цветом). Обратим внимание: этот вектор изменения скорости направлен вниз.
Построив аналогичные векторы для всех других положений шарика, мы убедимся, что все векторы изменения скорости одинаковы – по модулю и по направлению. Значит, свободный полёт тяжёлого шарика – равноускоренное движение, так как мгновенная скорость шарика меняется одинаково за одинаковые интервалы времени.