Вокруг нас множество движущихся тел. Их движение можно описать по-разному. Рассмотрим, например, словесное описание движения поезда. Выехав из пункта А, поезд 2 часа ехал со скоростью 100 км/ч, затем 1 час стоял, и в пункт Б прибыл через 3 часа после возобновления движения, всё это время поддерживая скорость 50 км/ч.
Движение этого же поезда можно описать при помощи таблицы:
| Время t, ч | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Путь l, км | 0 | 100 | 200 | 200 | 250 | 300 | 350 |
По данным таблицы построим график, и мы получим описание движения при помощи графика. На нём три этапа: от 0 до 2 часов (движение со скоростью 100 км/ч), от 2 до 3 часов (стоянка) и от 3 до 6 часов (движение со скоростью 50 км/ч).
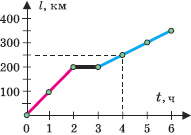
Каждый этап движения поезда на графике отражён прямой линией, которой в алгебре соответствует линейная функция y = kx + b, где k и b – числа. Применительно к нашей задаче про поезд, вместо y будем писать l, а вместо x будем писать t. Тогда мы получим описание движения формулами:
| Этап движения на графике | Интервал времени | Формула линии графика |
| I. (красный) | если 0 < t < 2 , то | l = 100 · t + 0 |
| II. (чёрный) | если 2 < t < 3 , то | l = 0 · t + 200 |
| III. (синий) | если 3 < t < 6 , то | l = 50 · t + 50 |
Как получаются эти формулы, мы изучим при решении задач, а пока убедимся, что они верные, например последняя. Значение t должно лежать в интервале от 3 до 6 часов. Возьмём значение 4 и подставим в формулу: l = 50 · 4 + 50. Вычисляем: 250 километров. В верхней таблице мы тоже видим, что за 4 часа поезд проехал 250 км. Взгляните и на график: для момента времени t = 4 ч получается путь l = 250 км.
Обобщим сказанное: рассмотренные способы описания движения – словесный, табличный, графический и формулами – равноправны. В зависимости от ситуации мы будем выбирать более удобный способ.
Кинематика (от греч. «кинематос» – движение) – раздел физики, изучающий способы математического описания движения тел без выяснения причин, вызвавших движение. Кинематика не интересуется тем, почему тело движется так, а не иначе. Она лишь отвечает на вопросы: как движение описать математически и что нового из такого описания можно почерпнуть?
Тело, собственными размерами которого в данных условиях можно пренебречь, называют материальной точкой. Например, если самолёт совершает перелёт по маршруту Москва–Сочи, диспетчер вполне может считать самолёт точкой (именно так он и отображается на экране радара). Однако тот же самолёт, выруливающий на взлётную полосу, точкой считать нельзя – надо учитывать, например, размах крыльев, чтобы не повредить другие самолёты или мачты освещения на месте стоянки.

В физике линию, которую «описывает» материальная точка при движении в пространстве, называют траекторией. Траектория может быть видимой или невидимой. Например, линия движения самолёта в небе часто видна (см. рисунок), а линия движения автомобиля по шоссе не видна. Заметим, что с точки зрения геометрии линия не имеет ширины. Поэтому, говоря о траектории движения любого тела, мы всегда считаем его материальной точкой.
По виду траекторий все движения тел делят на прямолинейные и криволинейные. Например, траектория падения мяча, выпущенного из рук, – отрезок прямой, полёта пушечного снаряда – часть параболы, а кончика маятника настенных часов – дуга, то есть часть окружности.