Значения физических величин можно не только сообщать в виде чисел, но и показывать на графике. Рассмотрим этот метод на примере физической величины «скорость», уже знакомой вам из курса математики. Проделаем опыт (см. рисунок).
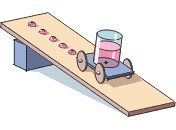 |
На верхнем конце длинной наклонной доски поставим тележку, с которой через равные интервалы времени падают капли воды, например, 2 раза в секунду. Наклон доски подберём так, чтобы, спустя некоторое время после начала движения тележки, кляксы на доске в среднем отмеряли равные части пути.
Чтобы построить график зависимости пути от времени и затем с его помощью вычислить скорость движения тележки, будем измерять отрезки пути с помощью клетчатой бумаги с масштабом 1 клетка – 1 см, положив её на доску. Мы увидим, что кляксы на бумаге расположатся, например, так, как показано на рисунке.
 |
Почему расстояния между кляксами всё-таки разные? Причин несколько: встряхивание тележки на неровностях доски, растекание воды по бумаге, влияние движения тележки на равномерность падения капель. Тем не менее мы перейдём к количественному изучению движения и заполним таблицу значениями:
| t, секунды | 0 | 0,5 | 1,0 | 1,5 | 2,0 | 2,5 | … |
| l, сантиметры | 0 | 5 | 11 | 14 | 19 | 26 | … |
Верхняя строка таблицы получается из расчёта, что «2 капли в секунду» это то же самое, что и «1 капля за полсекунды». Нижняя строка получается с помощью масштаба: 1 клетка – 1 см.
Теперь мы готовы построить график по экспериментальным точкам, используя пары значений в таблице как координаты точек. Нанесём их на координатную плоскость (см. рисунок). Мы видим, что точки сгруппировались вблизи воображаемой прямой линии, которую мы начертили пунктиром.
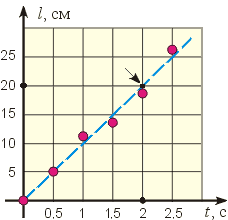 |
Почему мы провели линию графика именно так? Во-первых, она проходит через «контрольную», то есть обязательную точку (0; 0). Во-вторых, пунктирная линия проведена «посередине», чтобы количество точек по разные стороны от неё было равным.
Чем же полезен график? Вы спросите: «разве в нём есть что-то новое, если мы его построили на основе чисел»? Да, график даёт и новую информацию.
Во-первых, линия графика усреднила значения, соответствующие каждой отдельной точке. Поэтому, взяв на этой линии любую удобную нам точку и рассчитав по её координатам скорость тележки, мы допустим меньшую погрешность, чем в том случае, если бы воспользовались координатами какой-либо отдельной кляксы. В качестве такой «удобной точки» можно, например, взять точку с координатами (2 с; 20 см). Тогда скорость тележки вычислится так: v = 20 см : 2 с = 10 см/с.
Во-вторых, по линии графика можно предсказать те значения физических величин, для которых мы не проводили измерений (или сомневаемся, что верно их провели).
В заключение заметим, что график зависимости пройденного пути от времени имеет вид прямой линии, только если в опыте наблюдается равномерное движение – движение, при котором за равные интервалы времени тело преодолевает равные части пути.