На обёртке шоколадки написано «масса 100 г», в календаре мы читаем «время восхода солнца 6 ч», а на упаковке с новогодними свечами «длина 20 см». Откуда появились эти числа?
Числовые значения всех величин появляются в процессе измерений. Измерить – значит сравнить с мерой, то есть образцом для сравнения. Так, мерой для массы шоколадки служат гири, мерой длины свечей – деления на линейке, а мерой времени восхода солнца – положение стрелки на циферблате часов.
 |
Гири с массами 0,5 кг и 1 кг или банки с объёмами 1 л и 3 л – это самостоятельные меры. Однако часто меры неотделимы от измерительных приборов. Например, деления шкалы – от линейки.
Итак, измерение – это сравнение свойств изучаемого тела или явления с мерой (часто с помощью измерительного прибора) и выражение результата в виде числа и выбранной для этого измерения единицы.
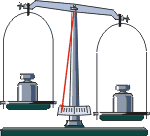 |
Все меры и/или измерительные приборы не являются абсолютно точными. Проделаем опыт. Возьмём две чугунные гири по 1 кг, которые используются в торговле. Поставим их на чаши лабораторных весов. Они покажут, что массы гирь не вполне одинаковы. Различие может достигать нескольких граммов!
Причин этому несколько: неточность изготовления гирь, их износ при длительном использовании, налипание частиц пыли и так далее. Эти и подобные им причины приводят к тому, что измерительные приборы и меры всегда вносят в результат измерения некоторую неточность – погрешность.
Важно: наши действия с измерительными приборами и мерами тоже вносят в результат измерения некоторую погрешность.
Обратимся к рисунку. Слева показано измерение длины карандаша, когда мы смотрим на него спереди, например, сидя на стуле. А справа – измерение длины, когда мы смотрим на карандаш сверху, к примеру, склонившись над партой. Поэтому, несколько раз измеряя линейкой длину одного и того же карандаша, каждый из нас может получить отличающиеся результаты, например значения 18,7 см и 18,8 см. Каждое из них правильное.
  |
Итак, неточность измерительных приборов и мер, а также неточность наших действий с ними приводят к тому, что результат любого измерения всегда имеет погрешность.
Однако остаётся вопрос: какое же значение взять для записи результата измерения длины карандаша? Можно выбрать любое, но можно провести дополнительные измерения. То есть снова совместить конец карандаша с нулевой отметкой шкалы, а взгляд точнее направить на конец грифеля. Такой метод многократных измерений позволяет с большей уверенностью выбрать одно из значений длины карандаша.
Многократные измерения – не единственный способ уменьшить погрешность результата. Можно воспользоваться методом рядов. Например, чтобы измерить диаметр одной горошины, расположим 10 горошин в ряд и измерим его длину. Если её разделить на 10, мы получим средний диаметр одной горошины.