Закон всемирного тяготения был открыт англичанином И. Ньютоном в 1666г. Закон звучит следующим образом: сила гравитационного притяжения двух материальных точек прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними. В виде формулы это записывается так:
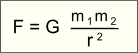 | m1, m2 – | массы взаимодействующих материальных точек, кг |
| r – | расстояние между ними, м | |
| G – | коэффициент, » 6.7·10-11 Н·м2/кг2 |
Убедиться в справедливости этой формулы нам поможет. Луна. Известно, что ее орбита почти круговая, и Луна делает один оборот за 27.3 суток. Известно также, что радиус орбиты Луны примерно в 60 раз больше радиуса Земли и составляет » 384 тыс км. Рассчитаем центростремительное ускорение Луны:
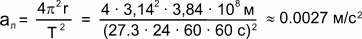
Вблизи Земли все тела, свободно летящие вниз или как угодно иначе, имеют одинаковое ускорение: 9.8 м/с2. Поделив это число на подсчитанное нами значение aл, мы получим » 3600 или » 602. То есть ускорение тел, свободно летящих вблизи Земли, в 602 раз больше ускорения тел, летающих на расстояниях, в 60 раз более далеких (как, например, Луна).
Вспомним, что ускорение свободного падения не зависит от массы тел. Значит, ускорение любого тела, удаленного от Земли на расстояние Луны, будет равно ускорению самой Луны. Тогда, согласно второму закону Ньютона, сила тяготяния этого тела к Земле на Земле тоже будет в 602 раз больше силы тяготения этого же тела к Земле на Луне. Таким образом мы убедились в справедливости второй части закона всемирного тяготения: сила тяготения между телами, обратно пропорциональна квадрату расстояния между ними.