Подставим в формулу второго закона Ньютона формулу определения ускорения. В результате получим:
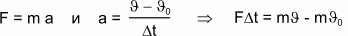
Обратите внимание, что в левой части равенства мы получили уже знакомую нам величину FDt – импульс силы. В правой части равенства тоже стоят знакомые нам величины: mJ – конечный импульс и mJ0 – начальный импульс тела. Разность mJ – mJ0 представляет собой изменение импульса тела. Поэтому полученную нами формулу мы прочтем так: импульс силы равен изменению импульса тела.
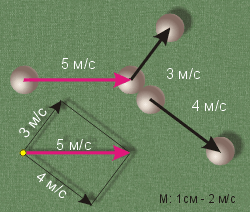
Рассмотрим два взаимодействующих тела, например, бильярдные шары. Запишем для них формулу третьего закона Ньютона
F1 = – F2
и выведенную нами формулу:
F1Dt = m1J1 – m1J01 и
F2Dt = m2J2 – m2J02
Подставив два последних равенства в формулу третьего закона Ньютона и проведя преобразования, получим:
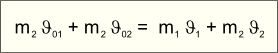
Это утверждение называют законом сохранения импульса: сумма импульсов тел до взаимодействия равна сумме их импульсов после взаимодействия. Однако закон справедлив лишь в том случае, если рассматриваемые тела взаимодействуют только друг с другом.
Быстро летящие бильярдные шары можно приблизительно считать взаимодействующими только друг с другом. Поэтому на чертеже выполяется векторное равенство: 5 м/с = 3 м/с + 4 м/с .