В 7 классе мы узнали, что тело может обладать потенциальной энергией потому, что взаимодействует с другими телами или частями одного и того же тела (см. § 5-д). Теперь дополним, что потенциальная энергия различных видов вычисляется по следующим формулам:
| При действии Fтяж | При действии Fупр |
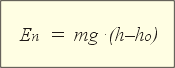 | 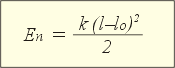 |
В левой формуле есть «нулевое» значение высоты, а в правой – «нулевое» значение длины упруго деформированного тела. Другими словами, значение потенциальной энергии зависит от выбора нулевого уровня энергии.
Почему именно так вычисляют различные потенциальные энергии тел? Оказывается, что если пользоваться этими формулами, начинает выполняться теорема об изменении потенциальной энергии:
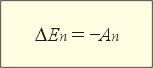 | DEп – изменение потенциальной энергии тела, Дж Aп – работа потенциальной силы, Дж |
Эта теорема читается так: изменение потенциальной энергии тела равно взятой с противоположным знаком работе потенциальной силы, действующей на тело. Эта теорема применяется и доказазывается только для потенциальных сил – зависящих от положения тел (или частей тела) и не зависящих от траектории, по которой тело (или части тела) совершают перемещение из начального положения в конечное.
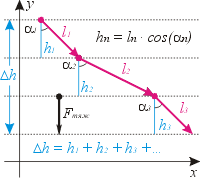
Поясним, какие силы будут потенциальными. Рассмотрим силу тяжести. Пусть она скатывает тело по склону с многочисленными изломами. Их можно считать множеством наклонных плоскостей, механическая работа на каждой из которых равна mg·ln·cos(an) = mg·hn. В этой формуле ln – длина n-ой «плоскости», hn – её высота, an – угол между векторами силы и перемещения.
Полная работа силы тяжести будет равна сумме:
Aтяж = mgh1 + mgh2 + … + mghn = mg ·(h1+h2+…+hn) = mg·Dh
Это равенство показывает, что работа силы тяжести зависит только от изменения положения тела и не зависит от формы и/или длины траектории движения тела. Поэтому сила тяжести – всегда потенциальная сила. Работа архимедовой силы тоже не зависит от траектории движения тела в среде, следовательно, архимедова сила – всегда потенциальная сила (если, конечно, среда однородна и тело всё время погружено целиком).
Вспомним, что сила упругости может как не подчиняться закону Гука (если деформация не упругая), так и подчиняться ему. В случае, если сила упругости подчиняется закону Гука, она потенциальна.
Работа силы трения скольжения зависит от формы и/или длины траектории тела, поэтому сила трения скольжения никогда не будет потенциальной. Работа силы трения покоя всегда обращается в ноль при возврате в исходную точку, значит, сила трения покоя – всегда потенциальная сила.
Формулы и теорема о потенциальной энергии легко проверяются опытами, одним из которых может быть следующая задача.
Задача. Из вертикальной пружинной пушки выстреливают шар, и он поднимается на высоту 1 м. Какую скорость шар имел при вылете?
Решение. Зная, что в верхней точке траектории скорость шара равна нулю, запишем теорему об изменении кинетической энергии:
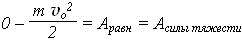
В полёте на шар действует только одна и потенциальная сила – сила тяжести. Приняв за нулевой уровень потенциальной энергии точку вылета шара, запишем теорему об изменении потенциальной энергии:
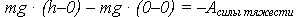
Упростив равенства и решив систему двух уравнений, получим:
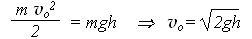
Ответ: начальная скорость шара при вылете из пушки была » 4,5 м/с.