В § 8-и мы начали знакомство с физической величиной «электрическое сопротивление». Продолжим его – проделаем опыт. Нам потребуются источник электроэнергии, амперметр, вольтметр, реостат и два резистора (две нихромовые спирали) с различными сопротивлениями.
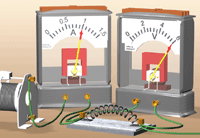 |
Соберём цепь, как показано на рисунке слева или на схеме в конце параграфа. Перемещая движок реостата, поочерёдно установим значения силы тока 0,4 А, 0,6 А, 0,8 А, 1 А. Запишем показания амперметра и вольтметра в таблицу. Повторим опыт, заменив резистор, и дополним таблицу:
| Первый резистор | Второй резистор | |||||||
| I , A | 0,4 | 0,6 | 0,8 | 1,0 | 0,4 | 0,6 | 0,8 | 1,0 |
| U , В | 1,6 | 2,4 | 3,2 | 4,0 | 2,4 | 3,6 | 4,8 | 6,0 |
| Поделив напряжение на силу тока, обнаружим закономерность: | ||||||||
| R = U/I | 4 | 4 | 4 | 4 | 6 | 6 | 6 | 6 |
Закономерность в том, что вне зависимости от значений напряжения и силы тока их частное остаётся постоянным для каждого резистора. Проверьте: после деления каждого числа строки (U, В) на расположенное над ним число строки (I, А) получаются одинаковые результаты во всех колонках левой половины таблицы: 4 В/А и во всех колонках правой половины таблицы: 6 В/А. Это показывает, что величина R является характеристикой именно изучаемого участка цепи – резистора.
Заметим, что эта закономерность всегда справедлива для металлических проводников в твёрдом или жидком состоянии; для других проводников она справедлива не всегда. Однако величину R, равную отношению U/I, всегда называют электрическим сопротивлением проводника независимо от его материала и состояния, а 1 В/А называют 1 Ом. Следовательно, 1 Ом – сопротивление такого проводника, в котором возникнет ток 1 А, если на концах проводника напряжение 1 В.
Связь между величинами U, I, R обычно записывается в виде формулы, известной как закон Ома для участка цепи:
| I = | U | I – сила тока в участке цепи, А U – приложенное напряжение, В R – сопротивление участка цепи, Ом | |||
| R |
Чтобы выяснить, как следует прочитать эту формулу, вспомним знания по алгебре о видах пропорциональности величин.
| прямая пропорциональность: | Y = k · X | → | I = 1/R · U |
| обратная пропорциональность: | Y = k / X | → | I = U / R |
Из первой строки следует: при постоянном сопротивлении величина 1/R тоже постоянна, поэтому сила тока прямо пропорциональна напряжению на концах участка цепи. Из второй строки: при постоянном напряжении сила тока обратно пропорциональна сопротивлению участка цепи. Объединяя это, получаем формулировку закона Ома для участка цепи: сила тока в участке цепи прямо пропорциональна напряжению на его концах и обратно пропорциональна сопротивлению этого участка.
 |
Примечание. С точки зрения алгебры, формулу закона Ома можно записать в такой форме: U=I·R. Применим её для изучения цепи, изображённой на схеме. Допустим, клеммы A и B присоединены к источнику с напряжением 10 В, однако вольтметр позволяет измерить напряжение не более 6 В (см. рисунок в начале параграфа). Поэтому нам нужно создать падение напряжения на реостате на 4 В или более. Как это сделать? Чем правее мы смещаем движок, тем больше сопротивление реостата, и, согласно формуле U=I·R, больше напряжение на реостате, которое и называют падением напряжения. В результате на резисторе напряжение снижается и может стать менее 6 В, что нам и нужно.