В XIX веке независимо друг от друга, англичанин Д. Джоуль и россиянин Э. Ленц изучали нагревание проводников электрическим током и опытным путём обнаружили закономерность: количество теплоты, выделяющееся в проводнике с током, прямо пропорционально квадрату силы тока, сопротивлению проводника и времени прохождения тока.
Силами других учёных было выяснено, что это утверждение справедливо для любых проводников: твёрдых, жидких, газообразных. Поэтому закономерность получила название закон Джоуля-Ленца:
| Q = I² R t | Q – выделившееся количество теплоты, Дж I – сила электрического тока в проводнике, А R – сопротивление проводника, Ом t – время прохождения тока, с |
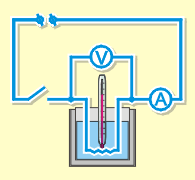 |
Справа показана схема установки, при помощи которой можно экспериментально проверить закон Джоуля–Ленца. Разделив напряжение на силу тока, по формуле R=U/I вычисляют сопротивление. Термометром измеряют повышение температуры воды. По формулам Q=I²Rt и Q=cmΔt° вычисляют количества теплоты, которые должны быть равны друг другу (с учётом погрешностей).
Для тех, кто интересуется физикой более глубоко, специально заметим, что закон Джоуля–Ленца можно получить не только экспериментально, но и вывести теоретическим путём, используя знакомые нам формулы.
| Согласно закону Ома | ||
| U = I · R | | | I = U / R |
| Согласно формуле работы тока | ||
| A = I·U·t = I·(I·R)·t | | | A = I·U·t = (U/R)·U·t |
| В итоге получаем: | ||
| A = (I²·R)·t | | | A = (U²/R)·t |
Мы получили сразу две новые формулы; выясним их физический смысл.
Левая формула A=I²Rt похожа на формулу закона Джоуля–Ленца, однако в левой её части стоит работа тока, а не количество теплоты. Что даст нам право считать эти величины равными? Для этого мы вспомним первый закон термодинамики (см. § 6-з) и выразим из него работу.
ΔU = Q + A следовательно A = ΔU – Q
Здесь ΔU – это изменение внутренней энергии нагреваемого током проводника; Q – количество теплоты, отданное проводником (на это указывает знак «–» впереди); A – работа, совершённая над проводником. Выясним, что это за работа.
Сам проводник неподвижен, но внутри него движутся электроны, наталкиваясь на ионы кристаллической решётки и передавая им часть своей кинетической энергии. Чтобы поток электронов не ослабевал, силы электрического поля должны постоянно совершать работу. Поэтому A – работа электрического поля по перемещению электронов проводника.
Обсудим теперь величину ΔU применительно к проводнику, в котором начинает идти ток. Проводник будет нагреваться, и его внутренняя энергия будет увеличиваться. По мере нагрева будет возрастать разность между температурами проводника и окружающей среды. Согласно закономерности Ньютона (см. § 6-л), будет расти мощность теплоотдачи. Вскоре это приведёт к тому, что температура проводника перестанет увеличиваться. И с этого момента внутренняя энергия проводника перестанет изменяться, то есть величина ΔU станет равной нулю.
Первый закон термодинамики для этого состояния запишется: A = –Q. Словами: если внутренняя энергия проводника не меняется, то работа тока полностью превращается в теплоту. Используя этот вывод, запишем все три формулы для вычисления работы тока в других видах:
| Q = I·U·t | Q = I²·R·t | Q = U²/R·t |
Эти формулы мы пока будем считать равноправными. Позднее мы узнаем, что средняя формула справедлива всегда (поэтому и носит название закона), а две крайние – только при определённых условиях (которые мы сформулируем в старших классах).