Познакомимся с физической моделью нитяной маятник. Взгляните на рисунок. Вы видите кирпич, подвешенный на широкой ленте, и тяжёлый шарик, подвешенный на нити. Толкнём их рукой, и оба тела начнут совершать колебания – станут маятниками.
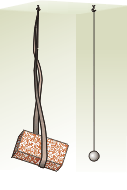
Изучить колебания – значит найти способы описания колебаний и выявить их закономерности. Удобен ли для этого кирпичный маятник? Конечно, нет. Во-первых, потому, что он большой, и при его качаниях будет велика сила сопротивления воздуха. Во-вторых, лента подвешена за два конца, и при качаниях её половины будут натягиваться неодинаково, из-за чего кирпич будет двигаться зигзагами. Тяжёлый шарик на нити более удобен для изучения колебаний.
Нитяным маятником называют тело на невесомой нерастяжимой нити, совершающее колебания. Для этой модели важно, чтобы размеры тела были малы по сравнению с длиной нити. В таком случае говорят: формой и размерами тела можно пренебречь (то есть в данных условиях не принимать их во внимание).
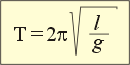
Опыты показывают: если на тело нитяного маятника действуют только сила тяжести и сила упругости, он совершает колебания с постоянным периодом. При этом, если амплитуда колебаний невелика по сравнению с длиной нити (говорят: маятник совершает малые колебания), то период колебаний нитяного маятника можно подсчитать по формуле, которая помещена в рамке.
Вы видите, что период малых колебаний нитяного маятника не зависит от его массы, а определяется лишь длиной нити l и коэффициентом g. Например, при увеличении длины нити в 4 раза, период колебаний маятника возрастёт в 2 раза (что равно √4 раз).
Рассмотрим вторую модель: пружинный маятник – тело на пружине, совершающее колебания. При этом важно, чтобы один конец пружины был закреплён, а её масса была мала по сравнению с массой тела (то есть массой пружины можно было бы пренебречь).
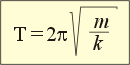
Опыты показывают: если на тело пружинного маятника действуют только сила тяжести и сила упругости, он совершает колебания с постоянным периодом. При этом, если амплитуда колебаний невелика по сравнению с длиной пружины (то есть она деформируется упруго), то период колебаний пружинного маятника можно подсчитать по формуле, которая помещена в рамке.
Итак, период малых колебаний пружинного маятника не зависит от коэффициента силы тяжести, а определяется лишь массой тела m и коэффициентом k, характеризующим жёсткость пружины. Например, при увеличении массы груза в 9 раз, период колебаний маятника возрастёт в 3 раза (что равно √9 раз).
Наряду со свободными колебаниями, когда маятник выведен из положения равновесия и предоставлен самому себе, существуют также вынужденные колебания и автоколебания. Обратимся к рисунку. Под гирей, висящей на пружине, расположен электромагнит. Если мы будем попеременно включать и выключать ток, то гиря начнёт совершать вынужденные колебания, частота которых зависит от частоты внешнего воздействия.

Однако маятник может сам регулировать поступление энергии, совершая автоколебания. Взгляните: средний провод зажат прищепкой и касается гири, пока она вверху. Ток, проходя через пружину, гирю, средний провод и электромагнит, намагничивает его сердечник. Притягиваясь, гиря движется вниз. Вскоре она отсоединяется от среднего провода, ток прекращается, и магнитное поле исчезает. Под действием пружины гиря поднимается вверх и снова замыкает цепь.