Движение жидкостей или газов представляет собой сложное явление. Для его описания используются различные упрощающие предположения (модели). В простейшей модели жидкость (или даже газ) предполагается несжимаемыми и идеальными (т. е. без внутреннего трения между движущимися слоями). При движении идеальной жидкости не происходит превращения механической энергии во внутреннюю, поэтому выполняется закон сохранения механической энергии. Следствием этого закона для стационарного потока идеальной и несжимаемой жидкости является уравнение Бернулли, сформулированное в 1738 г. Стационарным принято называть такой поток жидкости, в котором не образуются вихри. В стационарном потоке частицы жидкости перемещаются по неизменным во времени траекториям, которые называются линиями тока. Опыт показывает, что стационарные потоки возникают только при достаточно малых скоростях движения жидкости.
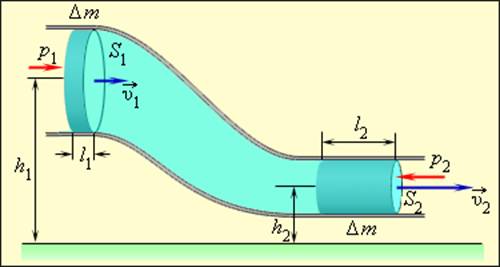
Рассмотрим стационарное движение идеальной несжимаемой жидкости по трубе переменного сечения (рис. 1.22.1). Различные части трубы могут находиться на разных высотах.
|
Рисунок 1.22.1. Течение идеальной жидкости по трубе переменного сечения. ΔV1 = l1S1; ΔV2 = l2S2. Условие несжимаемости: ΔV1 = ΔV2 = ΔV |
За промежуток времени Δt жидкость в трубе сечением S1 переместится на l1 = υ1Δt, а в трубе сечением S2 – на l2 = υ2Δt, где υ1 и υ2 – скорости частиц жидкости в трубах. Условие несжимаемости записывается в виде:
ΔV = l1S1 = l2S2 или υ1S1 = υ2S2. |
Здесь ΔV – объем жидкости, протекшей через сечения S1 и S2.
Таким образом, при переходе жидкости с участка трубы с большим сечением на участок с меньшим сечением скорость течения возрастает, т. е. жидкость движется с ускорением. Следовательно, на жидкость действует сила. В горизонтальной трубе эта сила может возникнуть только из-за разности давлений в широком и узком участках трубы. Давление в широком участке трубы должно быть больше чем в узком участке. Если участки трубы расположены на разной высоте, то ускорение жидкости вызывается совместным действием силы тяжести и силы давления. Сила давления – это упругая сила сжатия жидкости. Несжимаемость жидкости означает лишь то, что появление упругих сил происходит при пренебрежимо малом изменении объема любой части жидкости.
Так как жидкость предполагается идеальной, то она течет по трубе без трения. Поэтому к ее течению можно применить закон сохранения механической энергии.
При перемещении жидкости силы давления совершают работу:
ΔA = p1S1l1 – p2S2l2 = p1S1υ1Δt – p2S2υ2Δt = (p1 – p2)ΔV. |
Работа ΔA сил давления равна изменению потенциальной энергии упругой деформации жидкости, взятому с обратным знаком.
Изменения, произошедшие за время Δt в выделенной части жидкости, заключенной между сечениями S1 и S2 в начальный момент времени, при стационарном течении сводятся к перемещению массы жидкости Δm = ρΔV (ρ – плотность жидкости) из одной части трубы сечением S1 в другую часть сечением S2 (заштрихованные объемы на рис. 1.22.1). Закон сохранения механической энергии для этой массы имеет вид:
E2 – E1 = ΔA = (p1 – p2)ΔV, |
где E1 и E2 – полные механические энергии массы Δm в поле тяготения:
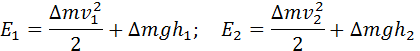
Отсюда следует:
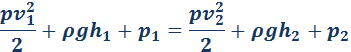
Это и есть уравнение Бернулли.
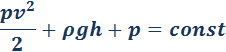
В частности, для горизонтально расположенной трубы (h1 = h2) уравнение Бернулли принимает вид:
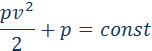
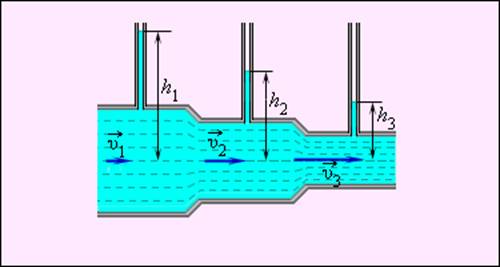
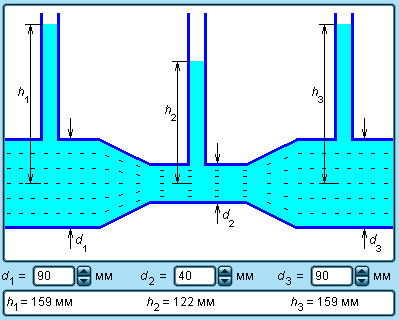
Величина p – статическое давление в жидкости. Оно может быть измерено с помощью манометра, перемещающегося вместе с жидкостью. Практически давление в разных сечениях трубы измеряется с помощью манометрических трубок, вставленных через боковые стенки в поток жидкости, так чтобы нижние концы трубок были параллельны скоростям частиц жидкости (рис. 1.22.2). Из уравнения Бернулли следует:
Давление в жидкости, текущей по горизонтальной трубе переменного сечения, больше в тех сечениях потока, в которых скорость ее движения меньше, и наоборот, давление меньше в тех сечениях, в которых скорость больше.
|
Рисунок 1.22.2. Измерение давления в потоке жидкости с помощью манометров. υ1 < υ2 < υ3; h1 > h2 > h3 |
 |
Модель. Течение идеальной жидкости. |
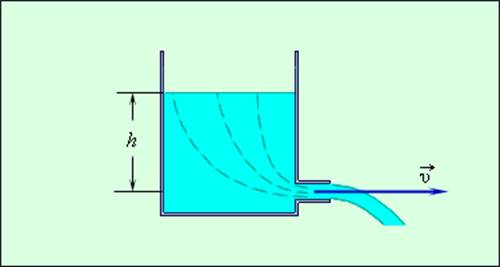
Если сечение потока жидкости достаточно велико, то уравнение Бернулли следует применять к линиям тока, т. е. линиям, вдоль которых перемещаются частицы жидкости при стационарном течении. Например, при истечении идеальной несжимаемой жидкости из отверстия в боковой стенке или дне широкого сосуда линии тока начинаются вблизи свободной поверхности жидкости и проходят через отверстие (рис. 1.22.3).
|
Рисунок 1.22.3. Истечение жидкости из широкого сосуда |
Поскольку скорость жидкости вблизи поверхности в широком сосуде пренебрежимо мала, то уравнение Бернулли принимает вид:
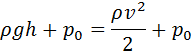
где p0 – атмосферное давление, h – перепад высоты вдоль линии тока. Таким образом,
Это выражение для скорости истечения называют формулой Торричелли. Скорость истечения идеальной жидкости из отверстия в сосуде такая же, как и при свободном падении тела с высоты h без начальной скорости.
В отличие от жидкостей, газы могут сильно изменять свой объем. Расчеты показывают, что сжимаемостью газов можно пренебречь, если наибольшие скорости в потоке малы по сравнению со скоростью звука в этом газе. Таким образом, уравнение Бернулли можно применять к достаточно широкому классу задач аэродинамики.
Одной из таких задач является изучение сил, действующих на крыло самолета. Строгое теоретическое решение этой задачи чрезвычайно сложно, и обычно для исследования сил применяются экспериментальные методы. Уравнение Бернулли позволяет дать лишь качественное объяснение возникновению подъемной силы крыла. На рис. 1.22.4 изображены линии тока воздуха при обтекании крыла самолета. Из-за специального профиля крыла и наличия угла атаки, т. е. угла наклона крыла по отношению к набегающему потоку воздуха, скорость воздушного потока над крылом оказывается больше, чем под крылом. Поэтому на рис. 1.22.4 линии тока над крылом располагаются ближе друг к другу, чем под крылом. Из уравнения Бернулли следует, что давление в нижней части крыла будет больше, чем в верхней; в результате появляется сила 
действующая на крыло. Вертикальная составляющая 
этой силы называется подъемной силой. Подъемная сила позволяет скомпенсировать силу тяжести, действующую на самолет, и тем самым она обеспечивает возможность полета тяжелых летательных аппаратов в воздухе. Горизонтальная составляющая 
представляет собой силу сопротивления среды.
|
Рисунок 1.22.4. Линии тока при обтекании крыла самолета и возникновение подъемной силы. α – угол атаки |
Теория подъемной силы крыла самолета была создана Н.Е. Жуковским. Он показал, что при обтекании крыла существенную роль играют силы вязкого трения в поверхностном слое. В результате их действия возникает круговое движение (циркуляция) воздуха вокруг крыла (зеленые стрелки на рис. 1.22.4). В верхней части крыла скорость циркулирующего воздуха складывается со скоростью набегающего потока, в нижней части эти скорости направлены в противоположные стороны. Это и приводит к возникновению разности давлений и появлению подъемной силы.
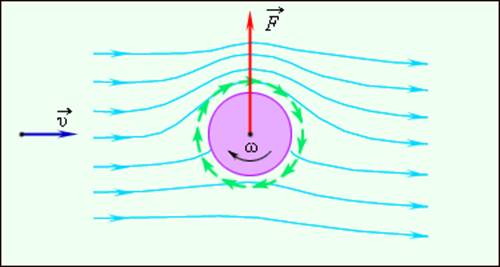
Циркуляция воздуха, обусловленная силами вязкого трения, возникает и вокруг вращающегося тела (например, цилиндра). При вращении цилиндр увлекает прилегающие слои воздуха, вызывая его циркуляцию. Если такой цилиндр установить в набегающем потоке воздуха, то возникнет сила бокового давления, аналогичная подъемной силе крыла самолета. Это явление называется эффектом Магнуса. Рис. 1.22.5 иллюстрирует обтекание вращающегося цилиндра набегающим потоком. Эффект Магнуса проявляется, например, при полете закрученного мяча при игре в теннис или футбол.
|
Рисунок 1.22.5. Обтекание вращающегося цилиндра набегающим потоком воздуха |
Итак, во многих явлениях аэродинамики существенную роль играют силы вязкого трения. Они приводят к возникновению циркулирующих потоков воздуха вокруг крыла самолета или вокруг вращающегося тела, к появлению силы сопротивления среды и т. д. Уравнение Бернулли не учитывает сил трения. Его вывод основан на законе сохранения механической энергии при течении жидкости или газа. Поэтому с помощью уравнения Бернулли нельзя дать исчерпывающего объяснения явлений, в которых проявляются силы трения. В этих случаях можно руководствоваться только качественными соображениями – чем больше скорость, тем меньше давление в потоке газа.
Особенно заметно проявляются силы вязкого трения при течении жидкостей. У некоторых жидкостей вязкость настолько велика, что применение уравнение Бернулли может привести к качественно неверным результатам. Например, при истечении вязкой жидкости через отверстие в стенке сосуда ее скорость может быть в десятки раз меньше рассчитанной по формуле Торричелли. При движении сферического тела в идеальной жидкости оно не должно испытывать лобового сопротивления. Если же такое тело движется в вязкой жидкости, то возникает сила сопротивления, модуль которой пропорционален скорости υ и радиусу сферы r:
Fсопр~v×r
Закон Стокса
Коэффициент пропорциональности в этой формуле зависит от свойств жидкости.
Поэтому, если тяжелый шарик бросить в высокий сосуд, наполненный вязкой жидкостью (например, глицерином), то через некоторое время скорость шарика достигнет установившегося значения, которое не будет изменяться при дальнейшем движении шарика. При движении с установившейся скоростью силы, действующие на шарик (сила тяжести 
выталкивающая сила 
и сила сопротивления среды 
), оказываются скомпенсированными, и их равнодействующая равна нулю.