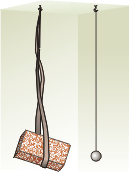
Пытаясь понять явления окружающего мира, мы поневоле считаем что-то главным, а что-то – второстепенным, отбрасываем несущественные детали, то есть моделируем. Познакомимся с одной из физических моделей – математическим маятником. Взгляните на рисунок. Слева изображен кирпич, подвешенный к потолку на широкой ленте. Справа нарисован медный шарик, подвешенный на нити. Толкнув их рукой, мы заставим тела совершать колебания. Кирпич и шарик станут маятниками.
В этой теме мы изучаем колебания. Изучаем – значит ищем способы описания как самих колебаний, так и закономерностей их протекания. Удобен ли для этих целей «кирпичный» маятник? Наверное, нет. Во-первых потому, что он большой, и при его качаниях будет велика сила сопротивления воздуха. Во-вторых, лента прикреплена к потолку в двух точках. Из-за этого при качаниях маятника ее половины будут натягиваться неодинаково, и кирпич будет раскачиваться «зигзагами». Медный шарик для изучения колебаний удобнее, но и его качания не идеальны. Поэтому и вводят модель.
Математическим маятником называют материальную точку, подвешенную на тонкой, невесомой и нерастяжимой нити. Например, камешек, подвешенный на нити длиной около метра, вполне можно принять за математический маятник.
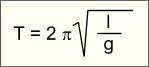
Если на тело не действуют никакие другие тела, кроме нити и Земли, то маятник совершает свободные колебания. Период малых колебаний такого маятника можно вычислить по формуле в рамке справа. Вы видите, что период колебаний математического маятника в данном месте Земли не зависит от его массы, а определяется лишь длиной нити. При увеличении ее длины, например, в 4 раза, период колебаний маятника возрастет в 2 раза.