Дедукция – это выведение частных умозаключений из более общих. Этим действием мы уже неоднократно пользовались. Рассмотрим еще один пример дедуктивного рассуждения.
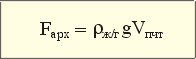 | Fарх | – архимедова сила, Н |
| rж/г | – плотность жидкости (газа), кг/м3 | |
| g | – коэффициент, Н/кг | |
| Vпчт | – объем погруженной части тела, м3 |
Запишем общую формулу, выражающую закон Архимеда:
Fарх = Wж
Вес вытесненной телом жидкости равен действующей на нее силе тяжести:
Wж = Fтяж = mжg
Масса вытесненной жидкости может быть найдена по формуле:
mж = rжVж
Подставляя формулы друг в друга, получим равенство:
Fарх = Wж = Fтяж = mжg = rжVжg
Выпишем начало и конец этого равенства:Fарх = rжgVж
Вспомним, что закон Архимеда справедлив для жидкостей и газов. Поэтому вместо обозначения «rж» более правильно использовать обозначение «rж/г» – плотность жидкости или газа. Также заметим, что объем жидкости, вытесненной телом, в точности равен объему погруженной части тела: Vж = Vпчт. С учетом этих уточнений получим:
Fарх = rж/гgVпчт
Итак, мы вывели частный случай закона Архимеда.
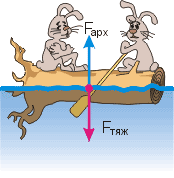
Продолжим изучение архимедовой силы дедуктивным путем. Посмотрите на рисунок. Поскольку полено находится в покое, то, согласно свойству уравновешенных сил, на полено действуют такие силы: сила тяжести и сила Архимеда. Так как они уравновешены, будет верным равенство:
Fарх = Fтяж
rжgVпчт = mтg
Разделим левую и правую части равенства на коэффициент «g»:
rжVпчт = mт
Вспомнив, что r = m/V Ю m = rV, получим равенство:
rжVпчт = rтVт
Преобразуем это равенство в пропорцию:
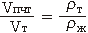
В левой части пропорции стоит дробь, которая показывает долю, которую составляет объем погруженной части тела от объема всего тела. Поэтому всю дробь можно назвать погруженной долей тела:
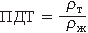
Все равенство можно прочитать так: погруженная доля плавающего тела равна отношению средней плотности тела к плотности окружающей его жидкости.
Используя эту формулу, предскажем, чему должна быть равна погруженная доля полена при его плавании в воде:
ПДТ (полена) = 500 кг/м3 : 1000 кг/м3 = 0,5
Число 0,5 означает, что плавающее в воде полено должно быть погружено наполовину. Так предсказывает теория, и это совпадает с практикой. Подтверждением этого служат плавающие тела – полено, айсберг и другие.