В статье Первый закон ньютона. Масса. Сила понятие массы тела было введено на основе опытов по измерению ускорений двух взаимодействующих тел: массы взаимодействующих тел обратно пропорциональны численным значениям ускорений
В векторной форме это соотношение принимает вид
Знак «минус» выражает здесь тот опытный факт, что ускорения взаимодействующих тел всегда направлены в противоположные стороны. Согласно второму закону Ньютона, ускорения тел вызваны силами 
и 
возникающими при взаимодействии тел. Отсюда следует:
Это равенство называется третьим законом Ньютона.
Тела действуют друг на друга с силами, равными по модулю и противоположными по направлению.
Силы, возникающие при взаимодействии тел, всегда имеют одинаковую природу. Они приложены к разным телам и поэтому не могут уравновешивать друг друга. Складывать по правилам векторного сложения можно только силы, приложенные к одному телу.
Рис. 1.9.1 иллюстрирует третий закон Ньютона. Человек действует на груз с такой же по модулю силой, с какой груз действует на человека. Эти силы направлены в противоположные стороны. Они имеют одну и ту же физическую природу – это упругие силы каната. Сообщаемые обоим телам ускорения обратно пропорциональны массам тел.
Рисунок 1.9.1. Третий закон Ньютона. |
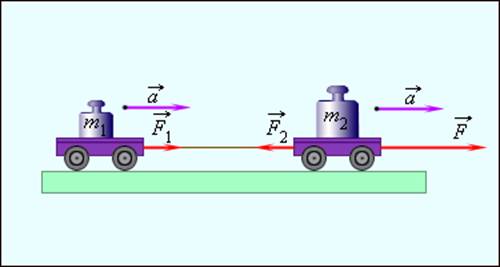
Силы, действующие между частями одного и того же тела, называются внутренними. Если тело движется как целое, то его ускорение определяется только внешней силой. Внутренние силы исключаются из второго закона Ньютона, так как их векторная сумма равна нулю. В качестве примера рассмотрим рис. 1.9.2, на котором изображены два тела с массами m1 и m2, жестко связанные между собой невесомой нерастяжимой нитью и двигающиеся с одинаковым ускорением 
как единое целое под действием внешней силы 
. Между телами действуют внутренние силы, подчиняющиеся третьему закону Ньютона: 
. Движение каждого тела зависит от сил взаимодействия между ними. Второй закон Ньютона, примененный к каждому телу в отдельности, дает:
Складывая левые и правые части этих уравнений и принимая во внимание, что 
и
получим:
Внутренние силы исключились из уравнения движения системы двух связанных тел.
|
Рисунок 1.9.2. Исключение внутренних сил |
